• Geografie
• Matematika
• IVT
• Ostatní

Matematika

Fotoshow

elektrárna Itaipu
Paraguay, Brazílie

krajina Badlands
USA

Info

Dnes je

svátek má .

Historie matematiky

STAROVĚK

Počáteční období, v němž se vytvářely kvantitativní a geometrické vztahy a operace s nimi, trvalo velmi dlouho. Až do 6. století př. n. l. šlo převážně o hromadění aritmetických pojmů, geometrických faktů a základních operací. Matematické znalosti se zaznamenávaly pouze různými systémy číslic a běžným jazykem, což brzdilo rychlejší rozvoj. Do 3. století př. n. l. chybí matematice jakákoliv speciální symbolika.

Mezopotámie

Z Mezopotámie pocházejí první písemné památky v dějinách lidstva a z období 2200 až 1800 př. n. l. se dochovalo velké množství matematických tabulek, které ukazují pokročilý stupeň rozvoje mezopotámské algebry i geometrie a také to, že matematika má opravdu dlouhou historii. V té době byly objeveny důležité algoritmy pro řešení rozmanitých úloh. Matematika byla schopna odpovědět na všechny požadavky tehdejší civilizace. Pro její další rozvoj patrně chyběly silnější podněty. Z dalšího období se takřka nezachovaly žádné matematické tabulky, a tudíž nelze posuzovat pozdější rozvoj matematiky. K násobení používali důmyslné komplety tabulek. Dělení převáděli na násobení převrácenou hodnotou, stanovení převrácené hodnoty jim opět umožňovaly tabulky. Při řešení úloh pracovali s přirozenými čísly a s kladnými šedesátinnými zlomky. Nepočítali s čísly iracionálními a zápornými. Řešení hledali pouze v oboru přirozených čísel a kladných šedesátinných zlomků.

Babylónské číslovky v klínovém písmu, svislý znak značí 1, vodorovný 10

V algebře počtáři řešili úlohy, které dnes vedou na rovnice lineární, kvadratické, kubické a bikvadratické i jejich soustavy. Objevily se dokonce úlohy vedoucí na rovnice osmého stupně, které nemají žádnou rozumnou aplikaci v tehdejší technické praxi. Byly patrně určeny na procvičování početních dovedností. Neznámé veličiny byly označovány jako délka a šířka, jejich součiny jako plocha. Někdy však byly termíny převzaty i z oblasti aritmetických operací (dělenec a dělitel, násobenec a násobitel atd.).

Samostatnou kapitolou jsou astronomické tabulky chaldejských počtářů, které svědčí o jejich nevšedních početních znalostech a dovednostech. Světu do dneška zanechali šedesátkovou soustavu (čas, úhly), rozdělení kruhu na 360 stupňů, dne na 24 hodin, hodiny na 60 minut a minuty na 60 sekund.

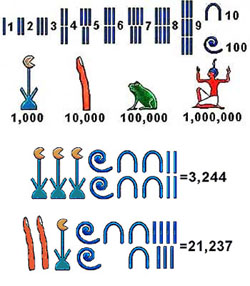číslicová symbolika v Egyptě

Egypt

Matematika starověkého Egypta se rozvíjela společně s rozvojem Egyptské civilizace od 4. tisíciletí př. n. l. Sloužila pouze k praktickým účelům, jako abstraktní věda nebyla ještě vyvinuta. Egypťané dokázali sčítat, odčítat, násobit, dělit, počítat se zlomky i řešit některé složitější aritmetické a geometrické problémy. Objevují se úvahy o výpočtech obsahu rovinných obrazců (obdélníku, trojúhelníku a kruhu).

Indie

Indická matematika byla ve své době až obdivuhodně rozvinutá. A způsobila velký zlom ve vývoji matematiky. Světu přinesla především poziční systém. Existovaly symboly pro prvních devět číslic. Desítkový charakter byl velmi rozvinutý. To vše představuje příznivé podmínky pro vytvoření poziční soustavy se základem 10. Obrovským objevem indických matematiků se stala nula: 0.

číslicová symbolika v Indii

Kromě toho skvěle ovládli počítání se zlomky. Jejich forma se téměř shodovala se současnou: čitatele psali nad jmenovatelem, ale nepoužívali zlomkovou čáru. Při operacích s celými čísly a se zlomky vyjadřovali celé čísla jako zlomky se jmenovatelem 1. Umocňování dvěma a třemi, znali a používali trojčlenku a mnoho dalšího.

Řecko

Kolébkou evropské kultury a vzdělanosti bylo starověké Řecko. V nových společenských podmínkách řecké otrokářské demokracie se začalo rozvíjet logické uvažování, což umožnilo vznik axiomaticko-deduktivní výstavby matematických teorií s logickým způsobem dokazování platnosti jednotlivých vět. Nejproslulejší knihou napsanou na tomto základě, se staly Euklidovy Základy, v originále Stoicheia' ze 3. století př. n. l.. Vzniká matematický důkaz, v Řecku v souvislosti s geometrií. Na vznik matematických pojmů a operací s nimi působily praktické podněty (obchod, peněžnictví, zeměměřičství, mořeplavby, astronomie…), zatímco k vytvoření matematické teorie, k systému výkladu matematiky, vedla snaha po uspořádání matematických poznatků, potřeba prokázání jejich platnosti a vyvoditelnosti z již dokázaných faktů.

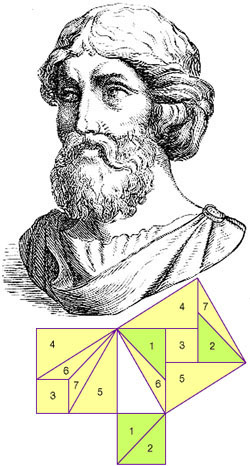Pythagoras

Velmi zajímavou postavou se stal Pythagoras, který tvrdil, že vše lze převézt na číselný princip a číslům přiřazoval různé vlastnosti. Za základ všeho považoval číslo, bod (bod jako prvek nejmenší vymezenosti - jeden bod je bod, dva body jsou úsečka, tři body tvoří trojúhelník, čtyři body prostorové těleso a součet těchto čísel dává číslo deset, které považoval za magickou konstrukci vesmíru a na tomto základě pak hledal on i jeho následovníci vztahy mezi věcmi). Pythagoras se narodil v Malé Asii na ostrově Samos. Po vpádu Peršanů se usadil na jihu Itálie a tam založil školu, která byla přístupná mužům i ženám a diskriminační chování bylo zakázáno. Na škole měl neomezenou autoritu. Velkou pozornost věnoval geometrii - Pythagorova věta: „Obsah čtverce sestrojeného nad přeponou pravoúhlého rovinného trojúhelníka je roven součtu obsahů čtverců nad jeho odvěsnami“. Není ale jasné, jestli je jejím autorem Pythagoras sám, nebo jeho žáci. Přívrženci jeho filozofie se nazývají pythagorejci, šlo o řecké filozofy, obývající řecké osady na jihu Itálie a příslušníky Pythagorovy školy.

O Eukleidově životě víme velmi málo. Narodil se v Řecku, studoval snad v Athénách na Platónově Akademii, kde se geometrii naučil od Eudoxa a Theaitéta. Král Ptolemaios I. (323 – 283 př. n. l.) ho povolal do nově založené Alexandrijské knihovny (či Musea), kde pracoval a snad také učil. Mezi jeho žáky snad patřil také Archimédés. Eukleidovým nejvýznamnějším dílem jsou třináctidílné „Základy“ („Stoicheia“) založené na systému ústředních axiomů geometrie. Ty další dva tisíce let určovaly evropské geometrické myšlení. Podává v nich také důkaz Pythagorovy věty a důkaz nekonečného množství prvočísel.

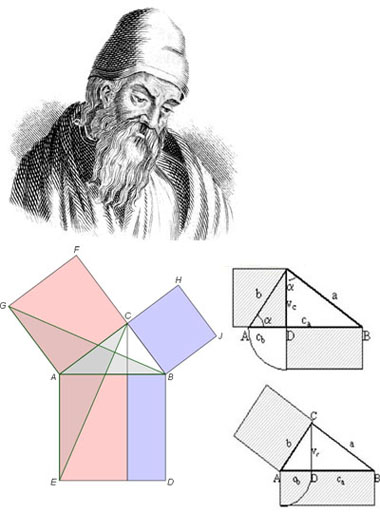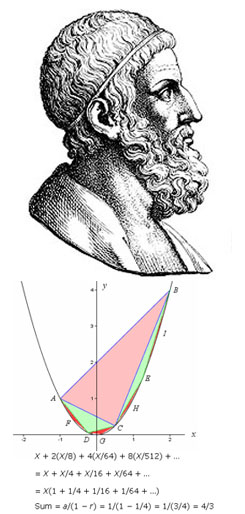Eukleides	Archimedes

Archimédés pocházel ze Syrákús a je jedním z nejvýznamnějších učenců antiky. Objevil mnoho zákonů matematiky a fyziky. V geometrii zavedl původně negeometrické pojmy jako těžiště, těžnice. Věnoval se metodám výpočtu ploch (především kruhu, elipsy a parabolické úseče) a objemů těles (zejména válce, kužele, koule, elipsoidu, paraboloidu). Stanovil objem rotačního paraboloidu, elipsoidu a hyperboloidu prakticky způsobem, který se dnes používá v integrálním počtu. Kolem roku 225 př. n. l. Archimédes zjistil, že obsah části paraboly odpovídá 4/3 obsahu trojúhelníku se stejnou základnou a výškou. Archimédes sestrojil nekonečnou posloupnost trojúhelníků počínaje trojúhelníkem o obsahu X (viz obr.) a dalšími menšími trojúhelníky vyplňujícími postupně oblast, která byla vymezena parabolou. Dostal nekonečnou posloupnost obsahů, jejich sečtení je prvním známým příkladem součtu nekonečné řady.

Své matematické výzkumy shrnul ve spise „De mechanicis propositionubis ad Eratosthenes methodus“ (O metodě mechanicky odvoditelných vět), objeveném až ve 20. století, v roce 1906. Jako matematik Archimédés odvodil obvod a obsah kruhu (určením přibližné hodnoty Ludolfova čísla). Jeho nejlepším odhadem bylo 3,1418 (chyba asi 0,0002). Je třeba si uvědomit, že Archimédes nemohl využít výhod algebraického a trigonometrického zápisu a desítkové soustavy čísel. Proto musel být výpočet velmi obtížný. Z vlastních matematických objevů si nicméně sám Archimédés pravděpodobně cenil nejvíce objevu poměru mezi objemy těles, kde do válce je vepsána koule, kouli je opsán kužel (jde o poměr 4:6:9) – tento objev údajně byl v grafické podobě ztvárněn na Archimédově náhrobním kameni.

STŘEDOVĚK

Zu Chongzhi

Čína

Čína byla až do 14. století v oblasti matematiky nejrozvinutější zemí světa. Např. Pythagorova věta byla zapsána v čínské matematické knize z 2. století př. n. l. V další důležité čínské matematické knize z 1. století jako první na světě byl objasněn pojem o záporném čísle a principy přičítání, odčítání, čínský matematik Zu Chongzhi určil v 5. století s velkou přesností hodnotu Ludolfova čísla. Dostal se k číslu 3,141 592 6. Jakou metodu přesně použil není známo.

Islámský svět

Arabská matematika byla nejvíce ovlivněna matematikou mezopotámskou, řeckou a indickou. Z indické matematiky převzala zápis čísel a algoritmy pro písemné počítání, z řecké matematiky abstraktní geometrii a myšlenku axiomatické výstavby matematiky, z mezopotámského a egyptského světa převzala tradici numericky náročných výpočtů a především důraz na užití matematiky v praktickém životě. Desítkový poziční systém pronikal pomalu na Blízký východ a byl používán vedle domácích systémů. Islámský svět se začal seznamovat s tzv. indickým systémem prostřednictvím al-Fázárího překladu díla Sinhásitas do arabštiny. Začali se používat číslice z Indie. Protože do Evropy se dostaly prostřednictvím Arabů, jsou dnes známé jako arabské číslice.

Al-Chwárizmí

V historii i v současnosti matematiky a informatiky hrály a hrají důležitou roli předpisy k řešení úloh, např. předpisy pro čtyři základní aritmetické operace s přirozenými čísly zapsanými v desítkové soustavě. Předpisy tohoto charakteru se zabýval počátkem 9. století arabský matematik Abdalláh Muhammad ibn Músa, al-Chwárizmí (nebo al-Chorezmí) al-Madžúsí, latinské zkomolení části jeho jména uvedlo do evropských jazyků slovo algoritmus. Al-Chwárizmí dovedl například geometricky řešit kvadratické rovnice a vymyslel také jednoduchý algoritmus pro násobení dvojciferného čísla, číslem jednociferným. V letech 800 a 825 napsal dvě díla, z nichž jedno byla početnice, které v latinském překladu začíná slovy „Algoritmi dicit“ („Tak praví Al Chwárízmí“). Zdánlivá záměna jmen vznikla patrně zkomolením při překladu z arabštiny do latiny. Druhým dílem byla učebnice algebry „Al-džabr wa-l-maqábala“ („Uspořádání“), která obsahovala nauku o řešení rovnic. Podle autora je rovnice uspořádána, pokud jsou všechny její členy kladné. Na takový tvar byly všechny rovnice převáděny, čímž autor definoval povolené operace s rovnicemi. Neznal algebru obecných čísel.

Evropa

Období středověku matematika, stejně jako ostatní vědy, v Evropě upadá. Někteří myslitelé a církevní matematici přesto dospěli k jistým důležitým výsledkům. Mikuláš Oresme (druhá polovina 14. století) studoval ze záliby mocniny s lomenými exponenty, ale hlavně napsal práci, v níž se zabývá závislostí mezi veličinami. Nanáší závisle proměnnou (latitudo — šířku) vůči nezávisle proměnné (longitudo — délce), kterou lze měřit. Je v tom druh přechodu od souřadnic na nebeské nebo zemské sféře (které znali již ve starověku) k moderním geometrickým souřadnicím. Jeho práce o tom byla několikrát vytištěna v letech 1482 až 1515 a pravděpodobně ovlivnila renesanční matematiky včetně Descarta.

Až do začátku 16. století nebyl učiněn žádný podstatný pokrok k překonání úrovně arabské a antické matematiky. První skutečně nové a původní výsledky přináší italští matematikové na počátku 16. století, pracující v oblasti řešení rovnic.

NOVOVĚKÁ EVROPSKÁ MATEMATIKA

Na počátku 16. století překročila evropská matematika rámec znalostí, které byly vytvořeny v antickém Řecku a národy orientu. Až do přelomu 16. a 17. století měla matematika jako předmět svého zkoumání hlavně kvantitativní veličiny a neměnné geometrické útvary. Scipio Del Ferro a jeho žáci na univerzitě v Bologni vytvořili teorii, která vedla k obecnému řešení kubické rovnice. V 15. století ovládali italští počtáři (praktikové) spolehlivě aritmetické výpočty včetně počítání s iracionálními čísly a italští malíři byli dobrými geometry. Vasari v knize Život malířů zdůrazňuje zvláštní zájem mnoha renesančních umělců o prostorovou geometrii.

Využití perspektivy v renesančním malířství

Změna společenských podmínek přináší i nové problémy, které má matematika řešit. Hodně podnětů dostává z fyzikální oblasti. Matematika pociťuje nutnost nacházet prostředky pro rychlejší zpracování získaných údajů. Pro výpočty se užívala různá počítadla, začátkem 17. století se staly důležitou pomůckou tabulky logaritmů (Napier, Bürgi, Briggs). Do popředí zájmu matematiků se dostává pohyb. Začínají se studovat proměnné veličiny a geometrická transformace. Galileo Galilei přichází s objevem, že balistická křivka je parabola, René Descartes roku 1637 ukazuje metodu, kterou lze za určitých podmínek popsat analyticky dráhu, po níž se pohybuje bod. Jeho analytická geometrie se stává předpokladem pro to, aby matematika odpověděla na otázku jak se pohybuje bod po své dráze (rovnoměrně nebo nerovnoměrně) a k řešení těchto problémů mechaniky přinášejí nezávisle na sobě ve druhé polovině 17. století nové matematické prostředky Leibniz a Newton infinitezimálním počtem. Později je aplikován i v geometrii (Gaspard Monge). Nástup měšťanstva a společenský vývoj v italských, francouzských, nizozemských i anglických městech s nástupem renesance přispěl ke snahám přiblížit matematické znalosti širším vrstvám společnosti a to v národních jazycích. V této době se objevují první české početnice, z nichž první jsou vydány roku 1530.

Vznik matematické analýzy

K dalšímu vývoji matematické analýzy (infinitezimální počet) od Archimédových začátků došlo až v 16. století, kdy mechanika přivedla matematiky k řešení problémů, jako bylo ohnisko gravitace. Johannes Kepler ve své práci o pohybu planet vypočetl obsah částí elipsy. Svoji metodu založil na představě plochy jako součtu úseček, která v podstatě byla metodou integrace. Pierre de Fermat také studoval maxima a minima. Zjistil, že funkce dosahuje svého maxima nebo minima, když je tečna křivky této funkce rovnoběžná s osou x. Svoji metodu popsal Descartovi tak, jak ji chápeme dnes: lokální maximum nebo minimum funkce se nachází v bodech, kde je derivace funkce rovna nule.

Johannes Kepler (1571 - 1630)	Pierre de Fermat (1601 - 1665)	René Descartes (1596 - 1650)

Skutečnými otci matematické analýzy jsou však Isaac Newton a Gottfried Wilhelm Leibniz. Newton ji vytvořil jako nástroj, který potřeboval pro své fyzikální výpočty. Nazýval ji flexí a její zápis i způsob práce s ní se o dnešního velmi lišil. Není jisté, kolik toho Leibniz o Newtonově metodě věděl (Newton své výsledky obvykle publikoval s velkým zpožděním), ale pár let po Newtonovi také přišel s tímto objevem, ale už s moderním zápisem (např. pro symbol integrálu), matematičtějším pojetím a pojmem „kalkulus“. Ve své době byl spor mezi těmito dvěma objeviteli značně vyhrocený a na mnoho dalších let představoval jablko sváru mezi „kontinentální“ a „ostrovní“ matematikou. Dnešní dějepisci přiznávají zásluhu oběma vědcům.

Gottfried Wilhelm Leibniz (1646 - 1716)	Isaac Newton (1643 - 1727)

Gaspard Monge (1746 - 1818)

Novověk učinil v oblasti geometrie dva důležité kroky: odhalil existenci neeuklidovských geometrií a vytvořil analytickou geometrii. Descart zavedením kartézské soustavy souřadnic objevuje metodu, jak analyticky, tj. prostřednictvím čísel a rovnic, zkoumat geometrické útvary. Díky tomuto objevu se v následujících staletích podaří vyřešit mnoho klasických geometrických problémů, např. nesestrojitelnost trisekce úhlu.

Stálé neúspěchy při logickém vyjadřování teorie rovnoběžek si vyžádaly ověřování základů euklidovské geometrie. Negováním pátého Euklidova postulátu o rovnoběžkách se u Lobačevského a Bolyaie objevila neeuklidovská geometrie jako matematicky zcela správná, ze svých axiomů odvoditelná a v okruhu své platnosti bezesporná teorie.

Za zakladatele deskriptivní geometrie je považován především Gaspard Monge, geometr, matematik, také znamenitý chemik, zabýval se fyzikou, mechanikou a vojenskou strategií. Byl váženým učitelem, profesorem a vědcem. Za Francouzské revoluce se podílel na zavedení metrické soustavy a od roku 1792 byl ministrem námořnictva. Během svého života se seznámil a spolupracoval s řadou významných osobností. Mezi jeho blízké přátele patřil i Napoleon Bonaparte, od kterého získal několik ocenění.

Ve vědecké revoluci 17. století narostla matematika do značné šíře a když pak na konci 18. století průmyslová revoluce přinesla velké množství technických problémů, byla matematika společně s fyzikou připravena k jejich řešení. Objevily se však také některé rozpory. Komplikované funkce, objevující se např. při zkoumání vedení tepla v různých materiálech, si vynutily zpřesnění pojmu funkce, limity, derivace apod. První kroky v tomto směru podnikli Augustin Louis Cauchy, Bernhard Riemann, český matematik Bernard Bolzano a posléze Karl Theodor Wilhelm Weierstrass.

Augustin Louis Cauchy (1789 – 1857)	Bernard Bolzano (1781 - 1848)	Karl Theodor Wilhelm Weierstrass (1815 - 1897)

Jedním z největších matematiků historie byl Carl Friedrich Gauss, autor více než sedmdesáti odborných vědeckých spisů. Známá je historka, kdy jako devítiletý školák dokázal během několika vteřin spočítat součet všech čísel od jedné do sta (5050). Ve své disertační práci na závěr jeho univerzitního studia pak Gauss podává jako první matematik důkaz tzv. základní věty algebry (tj. každá algebraická rovnice n-tého stupně a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀ = 0, kde a_n je různý od 0, má v oboru komplexních čísel alespoň jeden kořen). Na střední školách se dodnes učí jeho eliminační metoda pro řešení soustav lineárních rovnic. Gauss se proslavil také svými výzkumy v oblasti statistiky a počtem pravděpodobnosti (tzv. Gaussova křivka jako základní rozložení pravděpodobnosti), též se zabývá matematickou analýzou či funkcemi komplexní proměnné, významně se Gauss zabývá i teorií čísel – jeho nejznámějším dílem z oblasti matematiky je pak spis „Disquisitones aritmeticae“ (Pojednání o aritmetice, 1801).

Carl Friedrich Gauss (1777 - 1855)

V roce 1801 vypočítal dráhu planetky Ceres. Astronom Piazzi ji objevil 1. 1. 1801, ale pak se „ztratila“, Gauss jen na základě tří pozorování (a pomocí své metody nejmenších čtverců k vyrovnání chyb) určil její dráhu. Dne 7. 12. 1801 ji v udaném místě oblohy astronomoné znovu objevili. V letech 1821 - 1825 řídil Gauss triangulaci Hannoverska. Z této práce čerpal podněty pro studium konformních zobrazení (vytvořil Gaussovo konformní válcové zobrazení Země v příčné poloze, kde válcová plocha se dotýká středního poledníku, na němž nedochází k délkovému zkreslení) a diferenciální geometrie ploch. V geometrii je Gauss tím, kdo jako první odhaluje nedostatky v geometrii euklidovské – změnou pátého Euklidova axiomu objevuje principy hyperbolické geometrie (geometrie zakřiveného prostoru), nicméně tyto své objevy nikdy za svého života (patrně ze strachu z nepochopení a zesměšnění sebe sama) neuveřejní. Kromě matematiky, geometrie a astronomie se Carl Friedrich Gauss zabývá i fyzikou, ve svým fyzikálních výzkumech se přitom věnuje především zemského magnetismu (správně teoreticky určí polohu jižního magnetického pólu Země), společně s fyzikem W. E. Weberem se zabývá i studiem elektromagnetismu – v roce 1833 pak tito dva zkonstruují a postaví první linku elektromagnetického telegrafu na světě, a to v Göttingenu (je dlouhá 1,2 km).

Známá je i historka, která se stala na konci jeho života a týkala se jednoho z jeho prvních objevů. Ve starém Řecku bylo možné snadno zkonstruovat pravidelný trojúhelník a pětiúhelník, ale sedmnáctiúhelník umíme konstruovat až díky Gaussovi. Ostatní pravidelné mnohoúhelníky pak konstruujeme půlením úhlů těchto základních útvarů. Gauss byl svým objevem tak nadšen, že si přál vytesat pravidelný sedmnáctiúhelník na svůj vlastní náhrobek. Kameník mu to ale rozmluvil s tím, že vytesání takového obrazce je moc složité a laici by ho stejně považovali za kružnici...

Évariste Galois (1811 - 1835)

Neúspěch snah o přímé řešení obecných algebraických rovnic vyššího než čtvrtého stupně vedl k otázce, zda je takové řešení vůbec možné. Paolo Ruffini, Niels Henrik Abel a Évariste Galois ukázali, že takové řešení neexistuje a postavili algebru (do té doby jen nauku o řešení rovnic) na zcela jiný základ — teorie grup. V matematice se tak začaly z vnitřních problémů její výstavby tvořit teorie, které byly logicky správné a při tom často neodpovídaly žádné známé situaci z reálného světa. Začala nová etapa vývoje matematiky, kdy se předmětem zkoumání staly abstraktní kvantitativní vztahy a geometrické objekty, které čekaly a mnohé čekají na své praktické uplatnění.

částečně převzato z http://cs.wikipedia.org/
http://www.glouny.cz/matematika/mat_sem/priklady/